简介:
Treap,一种表现优异的BST
优势:
其较于AVL、红黑树实现简单,浅显易懂
较于Splay常数小,通常用于树套BST表现远远优于Splay
或许有人想说SBT,SBT我没有实现过,据说比较快
但是SBT、Splay以及旋转版Treap等BST都不可以比较方便地实现‘可持久化操作’
---> 旋转版Treap
本文主要介绍非旋转版Treap
介绍:
Treap=Tree+Heap
Treap是一颗同时拥有二叉搜索树和堆性质的一颗二叉树
Treap有两个关键字,在这里定义为:
1.key,满足二叉搜索树性质,即中序遍历按照key值有序
2.fix,满足堆性质,即对于任何一颗以x为根的子树,x的fix值为该子树的最值,方便后文叙述,定义为最小值
为了满足期望,fix值是一个随机的权值,用来保证树高期望为logn
剩下的key值则是用来维护我们想要维护的一个权值,此为一个二叉搜索树的基本要素
支持操作:
基本操作:
1.Build【构造Treap】【O(n)】
2.Merge【合并】【O(logn)】
3.Split【拆分】【O(logn)】
4.Newnode【新建节点】【O(1)】
可支持操作:
1.Insert【Newnode+Merge】【O(logn)】
2.Delete【Split+Split+Merge】【O(logn)】
3.Find_kth【Split+Split】【O(logn)】
4.Query【Split+Split】【O(logn)】
5.Cover【Split+Split+Merge】【O(logn)】
and more....
操作分析:
PS:如果没有看懂可以在最后看看我的代码
1.Build
让我们先来看看笛卡尔树,笛卡尔树同样是一颗同时拥有二叉搜索树和堆性质的一颗二叉树
---> 笛卡尔树【维基百科】
---> 笛卡尔树【百度百科】
笛卡尔树构造是和Treap完全一样的,如果key值是有序的,那么笛卡尔树的构造是线性的,所以我们只要把Treap当作一颗笛卡尔树构造就可以了
简要讲讲笛卡尔树:
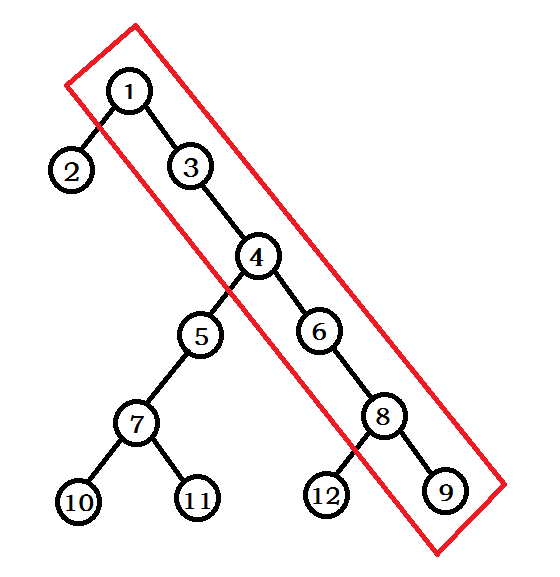
笛卡尔树构造时用栈维护了整棵树最右的一条链,每次在右下角处加入一个元素然后维护笛卡尔树的性质
图中,1、3、4、6、8、9为栈中元素,此时笛卡尔树满足所有性质,即在栈中元素fix值从1开始递增,假设此时我们在9的右儿子添加了一个13,若13的fix值小于栈顶元素9的fix,那么就开始退栈,停止退栈的条件有两个,满足任意一个即停止:
1.当前栈顶元素fix<13的fix【前面已经约定fix小的在上】
2.栈为空
若13的fix>3的fix并且<4的fix,那么上图会变为:
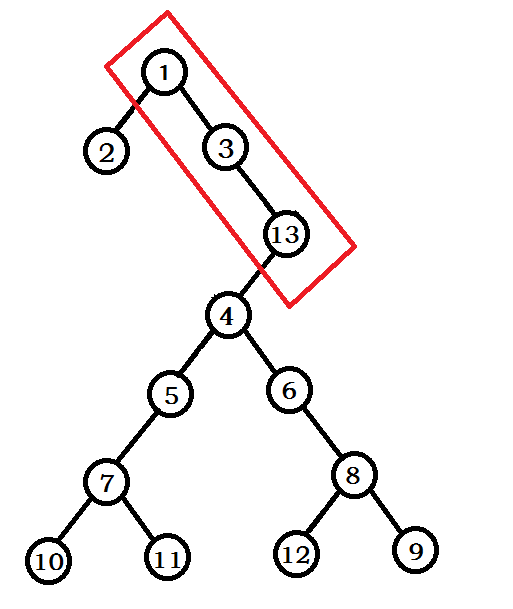
由于对于每个元素只会退栈一次,所以复杂度是O(n)
2.Merge
对于两个相对有序的Treap【若中序遍历为递增,即TreapA的最右下角也就是最大值小于TreapB的最左下角也就是最小值】,那么Merge的复杂度是O(logn)的;
对于两个相对无序的Treap,那么Merge只能启发式合并了。
那么Merge是如何操作的?
我们可以先来看看斜堆的Merge操作:
---> 斜堆【百度百科】
---> 可并堆【百度文库】
非常好理解,斜堆的Merge是一个递归操作:
若当前要Merge(A,B),若A的val<B的val,交换A,B指针;
然后A的右子树=Merge(A的右子树,B);
最后交换一下A的左右子树防止深度过深【upd 4.19:回来看了一下发现此处有错误,斜堆交换子树并不是为了防止树深度过深,而是满足插入期望。PS:读者可以思考一下为什么】
Treap的Merge也同理,只是需要注意满足中序遍历,因此不能交换左右子树,需要自行特判,代码也很简洁
3.Split
对于一个Treap,我们需要把它按照第K位拆分,那应该怎么做呢?
就像在寻找第K位一样走下去,一边走一边拆树,每次返回的时候拼接就可以了
由于树高是logn的,所以复杂度当然也是logn的
这样Treap有了Split和Merge操作,我们可以做到提取区间,也因此可以区间覆盖,也可以区间求和等等
除此之外因为没有了旋转操作,我们还可以进行可持久化,这个下文会讲到
4.Newnode
这个就不说了
5.可支持操作
一切可支持操作都可以通过以上四个基本操作完成:
Build可以用来O(n)构树还可以在替罪羊树套Treap暴力重构的时候降低一个log的复杂度
Merge和Split可用提取区间,因此可以操作一系列区间操作
Newnode单独拿出来很必要,这样在可持久化的时候会很轻松
可持久化
可持久化是对数据结构的一种操作,即保留历史信息,使得在后面可以调用之前的历史版本
对于可持久化,我们可以先来看看主席树(可持久化线段树)是怎么可持久化的:
---> 可持久化线段树【blog】
由于只有父亲指向儿子的关系,所以我们可以在线段树进入修改的时候把沿途所有节点都copy一遍
然后把需要修改的指向儿子的指针修改一遍就好了,因为每次都是在原途上覆盖,不会修改前一次的信息
由于每次只会copy一条路径,而我们知道线段树的树高是log的,所以时空复杂度都是nlog(n)
我们来看看旋转的Treap,现在应该知道为什么不能可持久化了吧?
如果带旋转,那么就会破环原有的父子关系,破环原有的路径和树形态,这是可持久化无法接受的
如果把Treap变为非旋转的,那么我们可以发现只要可以可持久化Merge和Split就可一完成可持久化
因为上文说到了‘一切可支持操作都可以通过以上四个基本操作完成’,而Build操作只用于建造无需理会,Newnode就是用来可持久化的工具
我们来观察一下Merge和Split,我们会发现它们都是由上而下的操作!
因此我们完全可以参考线段树的可持久化对它进行可持久化
每次需要修改一个节点,就Newnode出来继续做就可以了
*其他的问题
Q:Treap需不需要记录father指针?
A:看上去如果要可持久化的话是不能要的,但是我们知道不记录father指针会丧失一些BST的功能,如:
询问一个节点是第几大。
即所有自下而上的操作都不能实现。
那我们是否可以考虑加上father节点又能实现可持久化?答案是可以的!
主席给了我一种方法:
对每一个节点建立一个有序表,记录每次修改的版本信息,当儿子走向父亲的时候就可以在父亲的表中找到需要的信息,对于有序表的实现,我们可以在全局开一个hash表存储,这样复杂度依然是期望log(n)的!STQ 主席 ORL!!!
但是有个问题,我们必须要知道father节点恰好的修改时间,而我们往往不知道,往往需要寻找的是第K次修改之前的节点,怎么办呢?
还是可以的,我们可以牺牲一个log的复杂度在每个节点上建立一个线段树查询前驱。
然而我们还可以猎奇一点,现在我们的任务是:找到父亲的表中的第K次修改之前的节点,即寻找前驱。
寻找前驱。
因此我们可以在理论上做到 log(n)*log(log(n)) ,没错就是van Emde Boas tree
(其实在数据不大的情况下vEB的优势实在难以体现)
后附vEB & Treap代码
Code
/*
Treap[Merge,Split]
by Memphis
*/
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<ctime>
using namespace std;
#define maxn 2000005
#define rep(i,x,y) for(int i=x;i<=y;++i)
#define dep(i,x,y) for(int i=x;i>=y;--i)
struct Treap{
Treap *l,*r;
int fix,key,size;
Treap(int key_):fix(rand()),key(key_),l(NULL),r(NULL),size(1){}
inline void updata(){
size=1+(l?l->size:0)+(r?r->size:0);
}
}*root;
typedef pair<Treap*,Treap*> Droot;//用来Split返回两个根
inline int Size(Treap *x){return x?x->size:0;}//这样求size可以防止访问空指针
Treap *Merge(Treap *A,Treap *B){//合并操作
if(!A)return B;
if(!B)return A;
if(A->fix<B->fix){
A->r=Merge(A->r,B);
A->updata();
return A;
}else{
B->l=Merge(A,B->l);
B->updata();
return B;
}
}
Droot Split(Treap *x,int k){//拆分操作
if(!x)return Droot(NULL,NULL);
Droot y;
if(Size(x->l)>=k){
y=Split(x->l,k);
x->l=y.second;
x->updata();
y.second=x;
}else{
y=Split(x->r,k-Size(x->l)-1);
x->r=y.first;
x->updata();
y.first=x;
}
return y;
}
Treap *Build(int *a){//建造操作
static Treap *stack[maxn],*x,*last;
int p=0;
rep(i,1,a[0]){
x=new Treap(a[i]);
last=NULL;
while(p && stack[p]->fix>x->fix){
stack[p]->updata();
last=stack[p];
stack[p--]=NULL;
}
if(p) stack[p]->r=x;
x->l=last;
stack[++p]=x;
}
while(p) stack[p--]->updata();
return stack[1];
}
int Findkth(int k){//查找第K小
Droot x=Split(root,k-1);
Droot y=Split(x.second,1);
Treap *ans=y.first;
root=Merge(Merge(x.first,ans),y.second);
return ans->key;
}
int Getkth(Treap *x,int v){//询问一个数是第几大
if(!x)return 0;
return v<x->key?Getkth(x->l,v):Getkth(x->r,v)+Size(x->l)+1;
}
void Insert(int v){//插入操作
int k=Getkth(root,v);
Droot x=Split(root,k);
Treap *n=new Treap(v);
root=Merge(Merge(x.first,n),x.second);
}
void Delete(int k){//删除操作
Droot x=Split(root,k-1);
Droot y=Split(x.second,1);
root=Merge(x.first,y.second);
}
int a[maxn],M,x,y;
int main(){
freopen("bst.in","r",stdin);
freopen("bst.out","w",stdout);
scanf("%d",a);
rep(i,1,a[0]) scanf("%d",a+i);
sort(a+1,a+1+a[0]);
root=Build(a);
scanf("%d",&M);
while(M--){
char ch=getchar();
while(ch!='Q' && ch!='A' && ch!='D') ch=getchar();
scanf("%d",&x);
if(ch=='Q') printf("%d\n",Findkth(x));
if(ch=='A') Insert(x);
if(ch=='D') Delete(x);
}
}
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define maxn 5000005
#define inf 0x7f7f7f7f
#define rep(i,x,y) for(int i=x;i<=y;++i)
#define dep(i,x,y) for(int i=x;i>=y;--i)
int N,M,x;
inline int sqr(const int x){return x*x;}//平方
int power2(int x){//找到第一个大于等于x的二的整次幂
int ans=1;
for(;ans<x;ans<<=1);
return ans;
}
struct SQRT{//二的整次幂的开根上取和开根下取
int upper,lower;
}Sqrt[maxn];
/////////////////* van Emde Boas tree
int cluster_cnt,max_low,min_low,offset,succ_cluster,pred_cluster,first_cluster,summary_max;
struct vEB_tree;
vEB_tree *cluster[maxn];
struct vEB_tree{//以下部分解释详见《算法导论》
int p,u,Min,Max;
vEB_tree *summary;
inline int high(int x){return x/Sqrt[u].lower;}
inline int low(int x){return x%Sqrt[u].lower;}
inline int index(int x,int y){return x*Sqrt[u].lower+y;}
vEB_tree(){}
vEB_tree(int n):u(n){
p=cluster_cnt;
if(n>2){
cluster_cnt+=Sqrt[n].upper;
Min=cluster_cnt-1;
rep(i,p,Min)
cluster[i]=new vEB_tree(Sqrt[n].lower);
summary=new vEB_tree(Sqrt[n].upper);
}
Min=Max=inf;
}
int vEB_tree_Minimum(){return Min;}
int vEB_tree_Maximum(){return Max;}
bool vEB_tree_Member(int x){
if(x==Min || x==Max) return true;
if(u==2) return false;
return cluster[p+high(x)]-> vEB_tree_Member(low(x));
}
int vEB_tree_Successor(int x){
if(u==2){
if(x==0 && Max==1) return 1;
return inf;
}
if(Min<=N && x<Min) return Min;
max_low=cluster[p+high(x)]-> vEB_tree_Maximum();
if(max_low<=N && low(x)<max_low){
offset=cluster[p+high(x)]-> vEB_tree_Successor(low(x));
return index(high(x),offset);
}
succ_cluster=summary-> vEB_tree_Successor(high(x));
if(succ_cluster>N) return inf;
offset=cluster[p+succ_cluster]-> vEB_tree_Minimum();
return index(succ_cluster,offset);
}
int vEB_tree_Predecessor(int x){
if(u==2){
if(x==1 && Min==0) return 0;
return inf;
}
if(Max<=N && x>Max) return Max;
min_low=cluster[p+high(x)]-> vEB_tree_Minimum();
if(min_low<=N && low(x)>min_low){
offset=cluster[p+high(x)]-> vEB_tree_Predecessor(low(x));
return index(high(x),offset);
}
pred_cluster=summary-> vEB_tree_Predecessor(high(x));
if(pred_cluster>N){
if(Min<=N && x>Min) return Min;
return inf;
}
offset=cluster[p+pred_cluster]-> vEB_tree_Maximum();
return index(pred_cluster,offset);
}
inline void vEB_empty_tree_Insert(int x){Min=Max=x;}
void vEB_tree_Insert(int x){
if(Min>N) vEB_empty_tree_Insert(x);
else{
if(x<Min) swap(x,Min);
if(u>2){
if(cluster[p+high(x)]-> vEB_tree_Minimum()>N){
summary-> vEB_tree_Insert(high(x));
cluster[p+high(x)]-> vEB_empty_tree_Insert(low(x));
}else
cluster[p+high(x)]-> vEB_tree_Insert(low(x));
}
if(x>Max) Max=x;
}
}
void vEB_tree_Delete(int x){
if(Min==Max) Min=Max=inf;
else{
if(u==2){
if(x==0) Min=1;
else Min=0;
Max=Min;
}else{
if(x==Min){
first_cluster=summary-> vEB_tree_Minimum();
x=index(first_cluster,cluster[p+first_cluster]-> vEB_tree_Minimum());
Min=x;
}
cluster[p+high(x)]-> vEB_tree_Delete(low(x));
if(cluster[p+high(x)]-> vEB_tree_Minimum()>N){
summary-> vEB_tree_Delete(high(x));
if(x==Max){
summary_max=summary-> vEB_tree_Maximum();
if(summary_max>N) Max=Min;
else
Max=index(summary_max,cluster[p+summary_max]-> vEB_tree_Maximum());
}
}else
if(x==Max)
Max=index(high(x),cluster[p+high(x)]-> vEB_tree_Maximum());
}
}
}
}*root;
void Initialization(int n){//初始化
for(int i=0;(1<<i)<=n;++i){
Sqrt[1<<i].lower=1<<i/2;
Sqrt[1<<i].upper=1<<i/2+i%2;
}
root=new vEB_tree(n);//构造vEB tree
}
int main(){
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
scanf("%d",&N);
Initialization(power2(N));
rep(i,1,N){
scanf("%d",&x);
root-> vEB_tree_Insert(x-1);
}
int opt,x;
rep(i,1,N){
scanf("%d%d",&opt,&x);
if(opt==1) root-> vEB_tree_Insert(x-1);
if(opt==2) root-> vEB_tree_Delete(x-1);
if(opt==3) printf("%d\n",root-> vEB_tree_Predecessor(x-1)+1);
if(opt==4) printf("%d\n",root-> vEB_tree_Successor(x-1)+1);
}
}
Thu, 22 May 2014 21:37:20 +0800
orz memphis
您说的“加上father节点又能实现可持久化”是指部分可持久化(Partially persistent, http://en.wikipedia.org/wiki/Persistent_data_structure#Partially_persistent)吗?如果是的话,有没有办法实现加上father节点并支持完全可持久化(Fully persistent)?
Fri, 23 May 2014 19:38:16 +0800
@hehe: Orz。fat node应该是部分可持久化,如果要更新以前的版本可能也可以?如果把每个节点上的fat node用可持久化线段树维护或许就可以了?我也不是很清楚,没有实现过,仅供参考
Fri, 23 May 2014 20:35:52 +0800
orz Memphis !!! =我ZJOI滚粗了再去研究这些吧。。。
Fri, 23 May 2014 21:17:35 +0800
@hehe: 我才是真滚粗>.<,等待您进队的好消息
Fri, 23 May 2014 21:35:02 +0800
啊。。。。被D了。。(您显然不知道我是谁= =)
Sat, 24 May 2014 15:18:47 +0800
ZJOI爆0了。。。
Sun, 04 Jan 2015 20:03:02 +0800
orz孟爷赛高
Wed, 14 Jan 2015 12:57:29 +0800
orz孟爷
Sun, 05 Apr 2015 17:54:37 +0800
orz 孟爷
Sat, 02 Jul 2016 11:15:57 +0800
orz孟爷
Wed, 07 Dec 2016 10:11:05 +0800
话说Delete(x);是不是应该写成Delete(Getkth(root,x));的说。。Orz可能是我sb了。。
Thu, 15 Sep 2022 23:40:23 +0800
History can guide learners to see trends and processes from a broader, holistic perspective and to understand them. Through History, they come into contact with other cultures and societies and in this way they gain a more holistic understanding of the contemporary world and their place in this broader context. Telugu Medium, AP SSC History Question Paper English Medium & Urdu Medium Students of the State Board can download the AP 10th History Model Paper 2023 Pdf with Answers designed based on the revised syllabus and curriculum of the course. Class teachers and leading institutional experts are designed and suggested the Part-A, Part-B, Part-C, and Part-D exams like SA-1, SA-2, FA-1, FA-2, FA-3, FA-4 along with Assignments.
Sat, 14 Jan 2023 15:02:08 +0800
you use a fantastic blog here! do you wish to earn some invite posts on my small blog? 바카라사이트
Mon, 13 Feb 2023 16:16:59 +0800
I am pleased that I detected this web site, precisely the right info that I was searching for! . 二手mac
=============================
Spot lets start on this write-up, I must say i think this fabulous website needs far more consideration. I’ll probably be once more to learn far more, thank you that information. 여우알바
Thu, 23 Feb 2023 00:12:37 +0800
When I originally commented I clicked the -Notify me when new comments are added- checkbox and today each time a comment is added I recieve four emails with the same comment. Is there that is it is possible to remove me from that service? Thanks! 여우알바